$ sqrt(x^2 – 1)

Determinare le soluzioni della seguente disequazione:

$ sqrt(x^2 – 1) < x + 3 $

Poiché il radicale è minore di un certo valore, dobbiamo impostare un sistema a tre disequazioni in questo modo:

$$
\left\{
\begin{array}{ll}
x^2 – 1 ≥ 0& \\
x + 3 > 0 & \\
(\sqrt{x^2 – 1})^2 < (x + 3)^2 &
\end{array}
\right.
$$

Cominciamo risolvendo la prima disequazione:

$ x^2 – 1 ≥ 0 $

Passiamo all’equazione associata e determiniamo le soluzioni:

$ x^2 – 1 = 0 $

$ x^2 = 1 to x = ± 1 $

Prendiamo come soluzioni gli intervalli esterni alle radici, dato che la disequazione è maggiore o uguale a zero:

$ S : x ≤ – 1 ∨ x ≥ 1 $

La seconda disequazione è di risoluzione immediata:

$ x + 3 > 0 to x > – 3 $

Passiamo ora alla terza:

$ (sqrt(x^2 – 1))^2 < (x + 3)^2 $

$ x^2 – 1 < x^2 + 9 + 6x $

$ x^2 – 1 – x^2 – 9 – 6x < 0 $

$ – 10 – 6x < 0 $

$ – 6x < 10 to 6x > – 10$

$ x > – (10)/6 to x > – 5/3 $

Torniamo al sistema e determiniamo le sue soluzioni:

$$
\left\{
\begin{array}{ll}
x ≤ – 1 ∨ x ≥ 1 & \\
x > – 3 & \\
x > – 5/3 &
\end{array}
\right.
$$

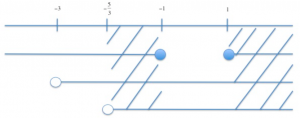
$ S : – 5/3 < x ≤ – 1 ∨ x ≥ 1 $

$ sqrt(x^2 – 1) < x + 3 $